Distributions of words across narrative time in 27,266 novels

Over the course of the last few months here at the Literary Lab, I've been working on a little project that looks at the distributions of individual words inside of novels, when averaged out across lots and lots of texts. This is incredibly simple, really -- the end result is basically just a time-series plot for a word, similar to a historical frequency trend. But, the units are different -- instead of historical time, the X-axis is what Matt Jockers calls "narrative time," the space between the beginning and end of a book.

In a certain sense, this grew out of a project I worked on a couple years ago that did something similar in the context of an individual text -- I wrote a program called Textplot that tracked the positions of words inside of novels and then found words that "flock" together, that show up in similar regions of the narrative. This got me thinking -- what if you did this with lots of novels, instead of just one? Beyond any single text -- are there general trends that govern the positions of words inside of novels at a kind of narratological level, split away from any particular plot? Or would everything wash out in the aggregate? Averaged out across thousands of texts -- do individual words rise and fall across narrative time, in the way they do across historical time? If so -- what's the "shape" of narrative, writ large?

This draws inspiration, of course, from a bunch of really interesting projects that have looked at different versions of this question in the last couple years. Most well-known is probably Matt Jockers' Syuzhet, which tracks the fluctuation of "sentiment" across narrative time, and then clusters the resulting trend lines into a set of archetypal shapes. Andrew Piper, writing in New Literary History, built a model of the "conversional" narrative -- based on the Confessions, in which there's a shift in the semantic register at the moment of conversion -- and then traced this signature forward through literary history. And, here at Stanford, a number of projects have looked at the movement of different types of literary "signals" across the X-axis of narrative. The suspense project has been using a neural network to score the "suspensefulness" of chunks of novels; in Pamphlet 7, Holst Katsma traces the "loudness" of speech across chapters in The Idiot; and Mark Algee-Hewitt has looked at the dispersion of words related to the "sublime" across long narratives.

Methodologically, though, the closest thing is probably Ben Schmidt's fascinating "Plot Arceology" project, which does something very similar except with movies and TV shows -- Schmidt trained a topic model on a corpus of screenplays and then traced the distributions of topics across the scripts, finding, among other things, the footprint of the prototypical cop drama, a crime at the beginning and a trial at the end. I was fascinated by this, and immediately started to daydream about what it would look like to replicate it with a corpus of novels. But, picking up where Textplot left off -- what could be gained by taking a kind of zero-abstraction approach to the question and just looking at individual words? Instead of starting with a higher-order concept like sentiment, suspense, loudness, conversion, sublimity, or even topic -- any of which may or may not be the most concise way to hook onto the "priors" that sit behind narratives -- what happens if you start with the smallest units of meaning, and build up from there?

It's sort of the lowest-level version of the question, maybe right on the line where literary studies starts to shade into corpus linguistics. Which words are most narratologically "focused," the most distinctive of beginnings, endings, middles, ends, climaxes, denouements? How strong are the effects? Which types of words encode the most information about narrative structure -- is it just the predictable stuff like "death" and "marriage," or does it sift down into the more architectural layers of language -- articles, pronouns, verb tenses, punctuation, parts-of-speech? Over historical time -- do words "move" inside of narratives, migrating from beginnings to middles, middles to ends, ends to beginnings? Or, to pick up on a question Ted Underwood posed recently -- would it be possible to use this kind of word-level information to build a predictive model of narrative sequence, something that could reliably "unshuffle" the chapters in a book? It's like a "basic science" of narratology -- if you just survey the interior axis of literature in as simple a way as possible, what falls out?

Stacking texts

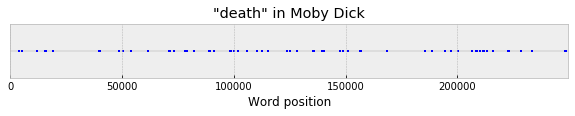
One nice thing about this question is that the feature extraction step is really easy -- we just need to count words in a particular way. At the lowest level -- for a given word in a single text, we can compute its "dispersion" across narrative time, the set of positions where the word appears. For example, "death" in Moby Dick:

So, just eyeballing it, maybe “death” leans slightly towards the end, especially with that little cluster around word 220k? Once we can do this with a single text, though, it’s easy to merge together data from lots of texts. We can just compute this over and over again for each novel, map the X-axis onto a normalized 0-1 scale, and then stack everything up into a big vertical column. For example, in 100 random novels:

Or, in 1,000:

And then, to merge everything together, we can just sum everything up into a big histogram, basically – split the X-axis into 100 evenly-spaced bins, and count up the number of times the word appears in each column. It’s sort of like one of those visualizations of probability distributions where marbles get dropped into different slots – each word in each text is a marble, and its relative position inside the text determines which slot the marble goes into. At the end, everything stacks up into a big multinomial distribution that captures the aggregate dispersion of the word across lots of texts. Eg, from the sample of 1,000 above:

This can then be expanded to all 27,266 texts in our corpus of American novels – 18,177 from Gale’s American Fiction corpus (1820-1930), and another 9,089 from the Chicago Novel Corpus (1880-2000), which together weigh in at about 2.5 billion words. For death:

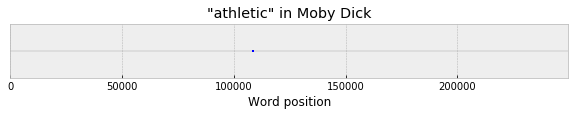
So it’s true! Not a surprise, but useful as a sanity check. Now, with “death,” it happened that we could already see a sort of blurry, pixelated version of this just with a handful of texts. The nice thing about this, though, is that it also becomes possible to surface well-sampled distributions even for words that are much more infrequent, to the degree that they don’t appear in any individual text with enough frequency to infer any kind of general tendency. (By Zipf’s law, this is a large majority of words, in fact – most words will just appear a handful of times in a given novel, if at all.) For example, take a word like “athletic,” which appears exactly once in Moby Dick, about half-way through:

And, even in the same sample of 1,000 random novels, the data is still very sparse:

If you squint at this, maybe you can see something, but it’s hard to say. With the full corpus, though, the clear trend emerges:

"Athletic" -- along with a great many words used to describe people, as we'll see shortly -- concentrates really strongly at the beginning of the novel, where characters are getting introduced for the first time. If someone is athletic, it tends to get mentioned the first time they appear, not the second or third or last.

Significance, "interestingness"

Are these trends significant, though? For "death" and "athletic" they certainly look meaningful, just eyeballing the histograms. But what about for a word like "irony":

Which looks much more like a flat line, with some random noise in the bin counts? If we take the null hypothesis to be the uniform distribution – a flat line, no relationship between the position in narrative time and the observed frequency of the word – then the simple way to test for significance is just a basic chi-squared test between the observed distribution and the expected uniform distribution, where the frequency of the word is spread out evenly across the bins. For example, “death” appears 593,893 times in the corpus, so, under the uniform assumption, we’d expect each of the 100 bins to have 1/100th of the total count, ~5,938 each. For “death,” then, the chi-squared statistic between this theoretical baseline and the observed counts is ~16,925, and the pvalue is so small that it literally rounds down to 0 in Python. For “athletic,” chi-squared is ~1,467, with p also comically small at 3.15e-242. Whereas, for “irony” – chi-squared is 98, with p at 0.49, meaning we can’t say with confidence that there’s any kind of meaningful trend.

Under this, it turns out that almost all words that appear with any significant frequency are non-uniform. If we skim off the set of all words that appear at least 10,000 times in the corpus (of which there are 10,908 in total) – of these, 10,513 (96%) are significantly different from the uniform distribution at p<0.05, 10,227 (94%) at p<0.01, and 9,815 (90%) at p<0.001. And even if we crank the exponent down quite a lot - at p<1e-10, 7,830 (72%) words still reject the null hypothesis. What to make of this? I guess there's some kind of very high (or low) level insight here - narrative structure does, in fact, manifest at the level of individual words? Which, once the numbers pop up in the Jupyter notebook, is one of those things that seems either interesting or obvious, depending on how you look at it. But, from an interpretive standpoint, the question becomes - if everything is significant, then which words are the most significant? Which words are the most non-uniform, the most surprising, which encode the most narratological information? Where to focus attention? How to rank the words, essentially, from most to least interesting?

This seemed like a simple question at first, but over the course of the last couple months I’ve gone around and around on it, and I’m still not confident that I have a good way of doing this. I think the problem, basically, is that this notion of “interestingness” or “non-uniformity” is actually less cut-and-dry that it seemed to me at first. Specifically, it’s hard to meaningfully compare words with extremely different overall frequencies in the corpus. It’s easy to compare, say, “sleeping” (which is basically flat) and “ancient” (which has a huge spike at the beginning), both of which show up right around 100,000 times. But, it’s much harder to compare “ancient” and “the,” which appears over 100 million times, and represents slightly less than 5% of all words in all of the novels. This starts to feel sort of apples-to-oranges-ish, in various ways (more on this later), and is further confounded by the fact that the data gets so sparse at the very top of the frequency chart – since a small handful of words have exponentially larger frequencies than everything else, it’s harder to say what you’d “expect” to see with those words, since there are so few examples of them.

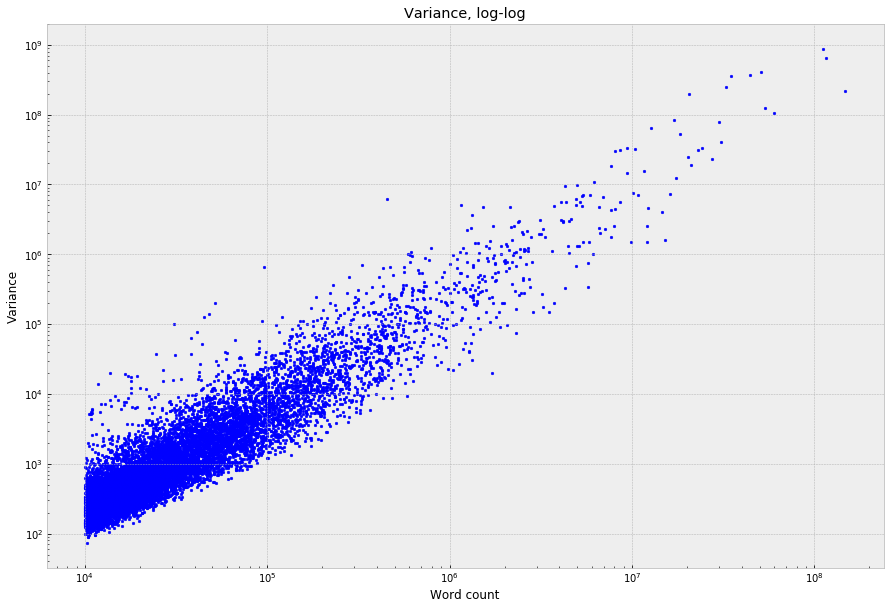
To get a sense of how this plays out across the whole dictionary – one very simple way to quantify the “non-uniformity” of the distributions is just to take the raw variance of the bin counts, which can then be plotted against frequency:

This is unreadable with the linear scales because the graph gets dominated by a handful of function words; but, on a log-log scale, a fairly clean power law falls out:

But, with that really wide vertical “banding,” which is basically the axis of surprise that we care about – at any given word frequency on the X-axis, words at the bottom of the band will have comparatively “flat” distributions across narrative time, and words at the top will have the most non-uniform / narratologically interesting distributions.

The nice thing about just using the raw variance to quantify this is that it’s easy to compare it against what you’d expect, in theory, at any given level of word frequency. For a multinomial distribution, the variance you’d expect to see for the count in any one of the bins is n * p (1-p), where n is the number of observations (the word count, in this context) and p is 1/100, the probability that a word will fall into any given bin under the uniform assumption. Almost all of the words fall above this line:

Which, to loop back, corresponds to the fact that almost all words, under the chi-squared test, appear not to come from the uniform distribution – almost all have higher variances than you’d expect if they were uniformly distributed.

I’m unsure about this, but – to get a crude rank ordering for the words in a way that (at least partially) controls for frequency, I think it’s reasonable just to divide the observed variances by the expected value at each word’s frequency, which gives a ratio that captures how many times greater a word’s actual variance is than what you’d expect if it didn’t fluctuate at all across narrative time. (Mathematically, this is basically equivalent to the original chi-squared statistic.)

So, then, if we skim off the top 500 words:

Does this make sense, statistically? I don’t love the fact that it still correlates with frequency – almost all of the highest-frequency words make the cut. But that might also just be surfacing something true about the high frequency words, which do clearly rise up higher above the line. (Counterintuitively?) There are other ways of doing this – namely, if you flatten everything out into density functions – that reward low-frequency words that have the most “volatile” or “spiky” distributions. But, these are problematic in other ways – this is a rabbit hole, which I’ll try circle back to in a bit.

Anyway, under this (imperfect) heuristic, here are the 500 most narratologically non-uniform words, ordered by the “center of mass” of the distributions across narrative time, running from the beginning to the end. There’s way too much here to look at all at once, but, in the broadest sense, it looks like – beginnings are about youth, education, physical size, (good) appearance, color, property, hair, and noses? And endings – forgiveness, criminal justice, suffering, joy, murder, marriage, arms, and hands? And the middle? I gloss it as a mixture of dialogism and psychological interiority – “say,” “think,” “feel,” and all the contractions and dialog punctuation marks – though it’s less clear-cut.

The really wacky stuff, though, is in the stopwords – which deserve their own post.

The feature extraction code for this project can be found here, and the analysis code is here. Thanks Mark Algee-Hewitt, Franco Moretti, Matt Jockers, Scott Enderle, Dan Jurafsky, Christof Schöch, and Ryan Heuser for helping me think through this project at various stages. Any mistakes are mine!