The Space of Poetic Meter

One of the goals of the Techne blog as a whole is to highlight technical issues in Digital Humanities---the kinds of in-the-weeds ideas that are interesting to specialists but don't necessarily make the cut of a final paper. It's easy to think of "technical issues" as the domain of the digital half of DH; but I think it's important to emphasize the technical nature of the humanities as well. Sometimes it's easy to forget in the new and complex DH world, or just in the STEM-centric environment of U.S. academia, that humanities researchers have *technical *expertise, and DH is best served when it tries to make advances in those areas as well as finding cool new digital methods.

To that end, I wanted to discuss an issue that came up a few years ago in the course of the Transhistorical Poetry Project, an early Literary Lab collaboration that included Ryan Heuser, Mark Algee-Hewitt, Jonny Sensenbaugh, Justin Tackett, and me. It started as a technical exploration of both programming and poetics, and led us to one of the most generative ideas of the project as a whole.

The original goal of the Transhistorical Poetry Project was to automate the detection of poetic form, loosely defined. The first benchmark was detecting the number of metrical feet in each poetic line, followed by extrapolating the "metrical scheme" of a given poem (both of which depended on metrical parsing software called "Prosodic," developed by Heuser, Josh Falk, and Arto Anttila).[1] That means, in the first instance, determining that the line "The brain is wider than the sky" has four feet, and that the Dickinson poem containing it alternates between four-foot and three-foot lines:

The Brain---is wider than the Sky---

For---put them side by side---

The one the other will contain

With ease---and You---beside---

In other words, the program was basically good enough to identify ballad meter, though we mostly stuck to labeling poems as "consistent" (like a sonnet, always five feet), "alternating" (like ballad meter) or "irregular" (everything else).[2]

Just this level of detail already unlocks new ways to study poetic history; in forthcoming papers, we'll be looking at, for instance, the history of pentameter in English poetry since the 16th century. But it's instantly clear to anyone who works on poetry that the results described above are a little unusual. Standard prosody doesn't really discuss "alternating 4 and 3", much less a generic "irregular" tag. Instead, it uses long-standing terminology for the metrical patterns within lines; sonnets, for example, are in iambic pentameter.

Since several of the members of the project work on poetry, we were especially curious about how our results could interact with four of the most common meters: iambic, trochaic, anapestic, and dactylic. We don't pretend that these are the only or best ways to categorize meter in English; but to us the balance of critical usage, and the poetic practice influenced by that usage, makes these categories worth exploring on their own terms.[3] In other words, we wanted to engage with the technical questions raised by ordinary prosody.

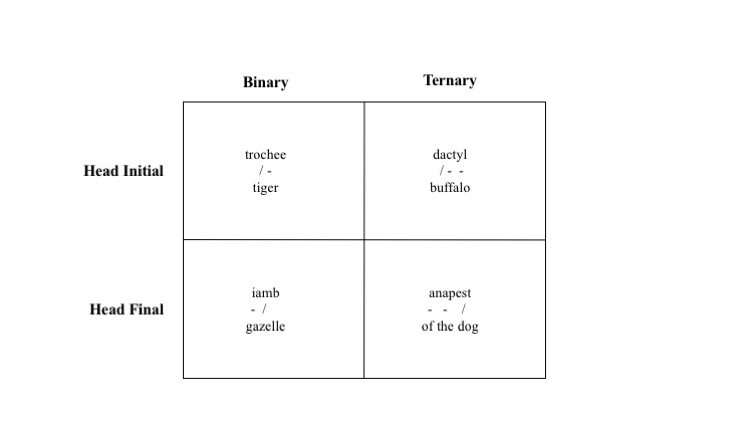
The first step, technical in the metrical sense, is to determine how these feet relate to each other. Essentially, they can be sorted by two criteria: 1. Does the stress come on the first part of the foot, or the last? 2. Does the foot have two beats, or three? These questions organize the feet like so :

Figure 1

(I couldn’t think of an anapestic animal.)

The next step, technical in the digital sense, was to operationalize these criteria. That is, on a programmatic basis, how can we tell: 1. Whether a foot is head-initial (falling) or head-final (rising)? 2. Whether a foot is binary or ternary?

Prosodic is pretty good at detecting which syllables in a line are stressed, which is the key to question one. Lines with a head-final rhythm should, generally speaking, start with an unstressed syllable, whereas lines with a head-initial rhythm should start with a stressed one. However, trochaic inversions are common enough that they could throw off the calculations for many poems that a human reader would call iambic. To get around that, we asked Prosodic about the fourth syllable in each line. This worked well, as you’ll see below, though it changes up the square a little.4 For question two, we simply check the frequency (in percentage terms) of consecutive weak syllables. Since ternary meters have two unstressed syllables per foot and binary meters only have one, we should see far more consecutive weak syllables in ternary meters.5

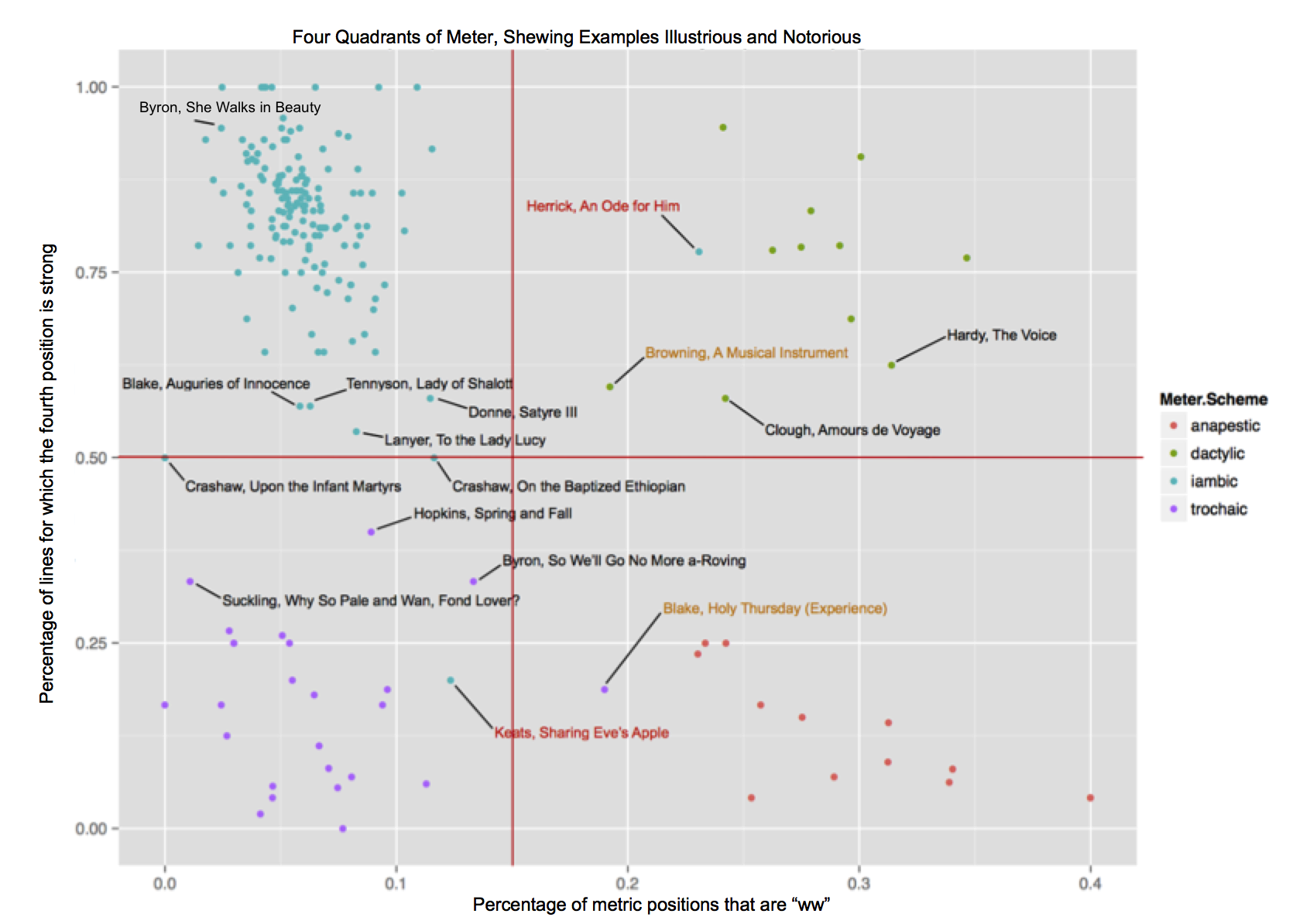
To test how well these operations worked, we assembled 205 poems that fit comfortably in each of the four meters—that is, they were consistently iambic, anapestic, etc. Sensenbaugh, Holst Katsma, and Zoya Lozoya scanned each of these poems line by line to confirm their metrical regularity. The colors in Figure 2 reflect these initial metrical tags.

Figure 2

The lines that cut the graph into quadrants are based on empirical observation; they divide the space in the way that maximizes the machine's accuracy relative to the initial tags. That accuracy is remarkably high: In this sample, we correctly classified 202 of the 205 poems, or 98.5%.[6] Even the borderline cases are often successes here: Richard Crashaw's "Upon the Infant Martyrs", for example, lies exactly between the iambic and trochaic quadrants; its first two lines are perfectly iambic, and its second two lines are perfectly trochaic:

To see both blended in one flood,

The mothers' milk, the children's blood,

Makes me doubt if heaven will gather

Roses hence, or lilies rather.[7]

At the beginning of the project, we joked that we wanted Prosodic to be as accurate as an undergraduate, and we feel that we succeeded---either inspiring or depressing, depending on your perspective.

At the same time, Crashaw's poem is exemplary of a key lesson from this graph. I've been speaking of the division of poems into four metrical categories, but there are not four positions here; there are hundreds, nearly as many as there are poems. Tennyson's "Lady of Shalott"  and Byron's "She Walks in Beauty" may both be iambic, but they clearly differ from each other according to the criteria we used to determine their iambic-ness---the distance between the two is substantial, even within the iambic quadrant. The "categories" are far more nuanced than four simple designations; to be precise, what we have here is a metrical space.

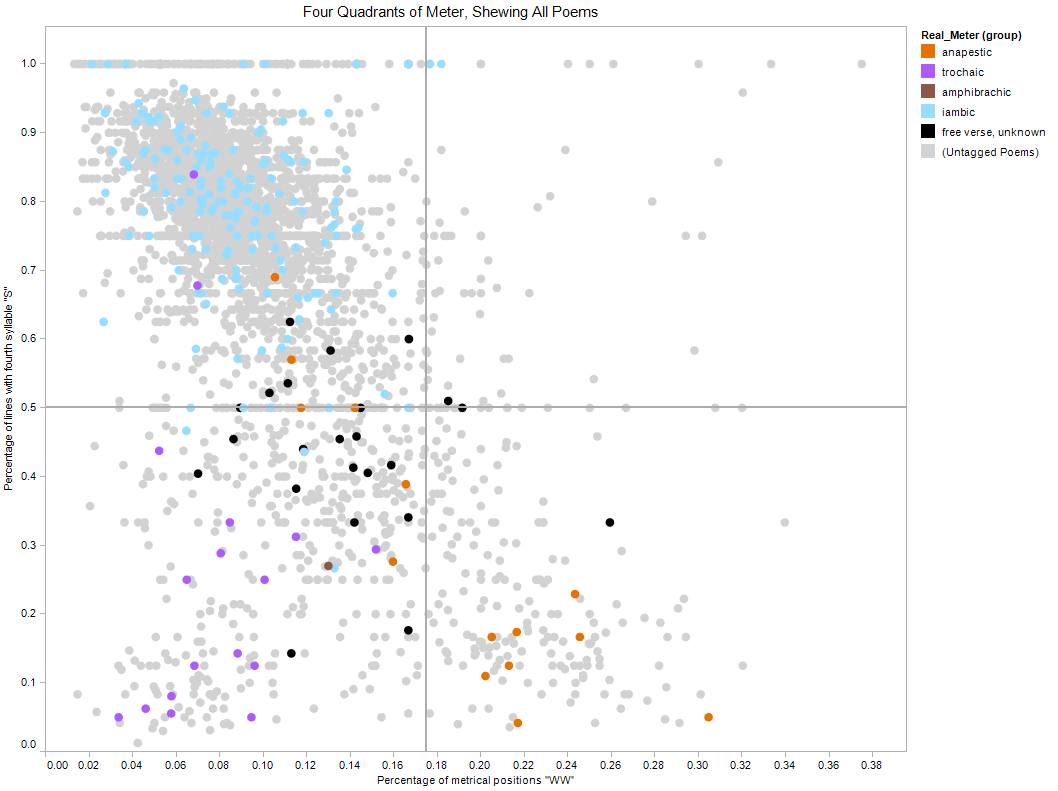
When we turned our attention to a larger archive of poems, we serendipitously discovered a new way to think about this metrical profusion:

Figure 3

Every dot is a poem; there are 6,400 in total on this graph. From these, we selected 238 at random and scanned them by hand; our conclusions are reflected in the colors you see here. Compared to our human tags, the program correctly identified 94% of poems.

With even more metrical variety in front of us, we noticed one poem the graph doesn't categorize. At the center of the dividing lines, sitting in none of the four quadrants, is Thomas Hood's "Lines to Miss F. Kemble, On the Flower Scuffle at Covent Garden Theatre," a comic poem published in 1832 in the Athenaeum. As it happens, this poem is maniacally unmetrical (or perhaps it's the more philosophical "ametrical")---even moreso than the free verse poems in our sample (in black), which often displayed a particular metrical tendency, even if "accidental." Here is the first stanza:

Well---this flower-strewing I must say is sweet

And I long, Miss Kemble, to throw myself considerably at your feet;

For you've made me a happy man in the scuffle when you jerk'd about the daisies;

And ever since the night you kiss'd your hand to me and the rest of the pit, I've been chuck full of your praises!

The rest of the poem (available here) continues very much in the same vein, structured by rhyme but hilariously difficult to read with any metrical regularity.[8] And this is just the exemplar of a general rule: If a poem is perfectly metrical according to these classical feet, it shows up near the corners of the graph---a perfectly trochaic poem will never have an accented fourth foot or two consecutive weak syllables. If a poem is all over the place, like Hood's, it will show up near his. If it is somewhere in between---like most poems---it will appear in the space between. And we find this to be true, empirically; the closer a poem is to the center, the more apt it is to be free verse or some other irregular form. Thus the Hood Distance of a poem---literally its distance from Hood's "Lines to Miss F. Kemble" on this graph---is a measure of the extent to which it exhibits the characteristics of one of these four basic feet, *but not the others---*that is, its metricality, or metrical regularity.[9]

On one hand, Hood Distance is a great example of a lesson that we encounter again and again in quantitative literary criticism: Things tend not to just be A or B, but to be some percentage A or B. That's what a trochaic inversion, for instance, really indexes in the first place---most sonnets aren't 100% iambic (or, in a sense, 100% sonnet). This graph gives us a way to see meter in particular not as a quality (either iambic or trochaic) but as a space of possibilities.

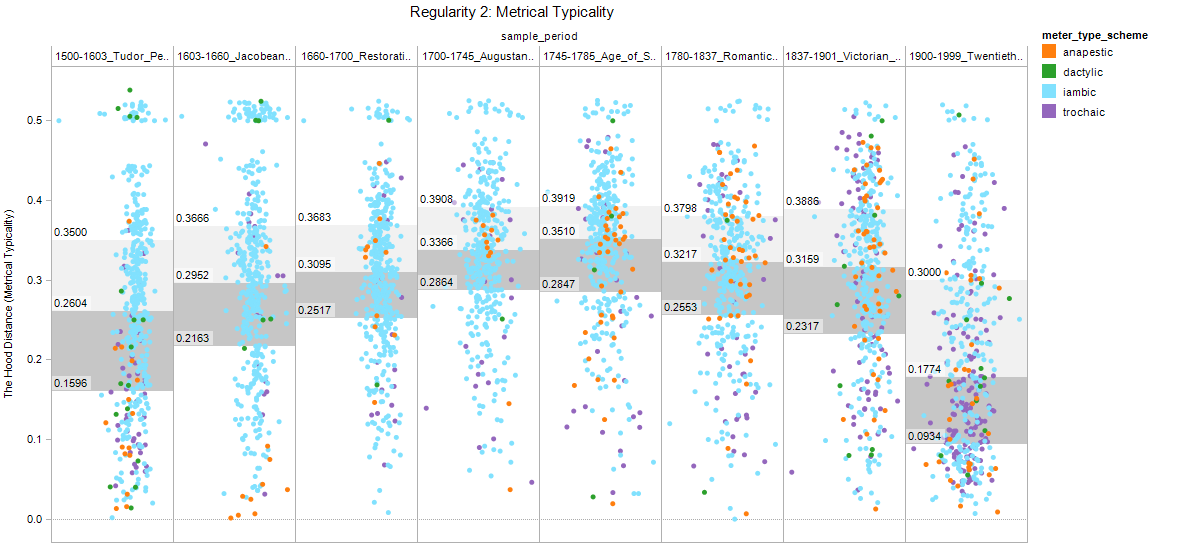
On the other hand, we believe that Hood Distance amounts to more than added nuance for an existing concept. It articulates a new concept, the range of formal variation from poems with a strongly defined base meter (like iambic ballads) to those with no particular base meter at all (like free verse poems). In short, Hood Distance means that the metricality of a poem, in this complex metrical space with its hundreds of realized possibilities, can be measured. We can track the history not just of things like pentameter, or even iambic pentameter, but metricality in general---the tendency of the poems of an era (or at any rate, the poems we can get from an era) to adhere to the prosodic rules that evolved alongside them. For example, here is the variation in Hood Distance we see over the course of some of the eras tagged in the Chadwyck-Healey poetry corpus:

Figure 4

Each dot here is a poem; the gray bars contain 50% of the poems in a given era, and the spot where they change color is the median Hood Distance for that era. The colors of the poems reflect the traditional, categorical designations of meter, but the changes in the distribution, the rise and fall of the median, show a new kind of poetic history: The rise and fall of metrical regularity. Starting in the Tudor period, Hood Distance increases through the eighteenth century; the Romantic Era then initiates a decline in regularity that persists as long as the data does, as clearly iambic and trochaic poems give way to more freewheeling meters. Like so many DH findings, this tracks roughly with what we "already knew"---but did we know it? Are you sure you wouldn't have picked the Augustan Age for peak regularity? What would you have said about the Victorian Era as against the Restoration? If knowledge is (more or less) true justified belief, we now have more empirical justification and a more precise sense of the truth, where neither were quite as possible before.

In the end, Hood Distance gives us a new lens for measuring a technical feature of poetics on the scale provided by digital research. And conceptually speaking, Hood Distance is not the only thing we can measure this way. In theory, we could track the distance from any poet, defining meter in terms of, say, a Dickinson distance. Or we could change the axes, putting, say, Hood Distance itself on one, and the percentage of line-ending rhymes on the other, to measure the license that rhyme gives (if any) to metricality. Meter is a complex structure that has varied widely in theory and practice over time, but this concept of spatial arrangement derived from programmatic analysis of thousands of poems enables us to construct frameworks for describing poetic history with the usual DH mixture of the very broad and the very specific. It's the D and the H as a dialectic; this metrical space is the synthesis of two kinds of technical exploration.

Notes

¹ Ryan Heuser, the primary programmer during this project, has written two approachable summaries of Prosodic for those who wish to use it, one more specific to this project, and one (more frequently updated) for more general use. For a more linguistics-oriented introduction to the software, see: Anttila, Arto, and Ryan Heuser. "Phonological and Metrical Variation across Genres." Proceedings of the Annual Meeting on Phonology 3 (2016). Web. Linguistic Society of America. Washington D.C., 2015. The paper is available here.

² I wanted to use the more thematically-appropriate "Split the lark and you'll find the music", but it's more typically Dickinsonian---i.e., too irregular to serve as an example of "perfect" meter.

³ We thought of including other feet, but as Jonny Sensenbaugh writes: "Although other classical metrical feet such as the spondee and the amphibrach exist, the existence of truly spondaic poems is doubted in linguistic theory (*Princeton Encyclopedia of Poetry and Poetics, *1352), and that of English amphibrachic poems both exceedingly rare and difficult to distinguish from anapestic or dactylic meter (45)".

⁴ Iambs and dactyls are stressed on the fourth syllable (-/-/ and /--/, respectively), whereas trochees and anapests are unstressed there (/-/- and --/-, respectively).

⁵ Here's a simplified explanation showing why this works: In Prosodic, a perfectly iambic line (with, let's say, four feet) would read "w-s-w-s-w-s-w-s"; a perfectly trochaic line would read "s-w-s-w-s-w-s-w". The "w-w" pair (the minimum unit of consecutive weak syllables) never appears in either line; even if an iambic or trochaic poem had a "mistake" here or there, that "w-w" pair would still be relatively rare. Compare a perfect anapestic line, "w-w-s-w-w-s-w-w-s-w-w-s", or a perfect dactylic line, "s-w-w-s-w-w-s-w-w-s-w-w". These are rife with the "w-w" pair, and even with variations here and there in the poem, the pair should still occur frequently.

⁶ On a line-by-line level, the accuracy was lower---59%. The accuracy for a poem as a whole, however, depends only on getting most of the lines right, so two or three lines of a sonnet can be mischaracterized as trochaic and the program will still place the poem in the iambic quadrant. In a loose sense, then, the overall metrical scheme of the poem influences the "interpretation" of individual lines---not too dissimilar from human reading.

⁷ Note that in British poetry of this period, "heaven" is usually treated as a one syllable word.

⁸ Note the italicized "is" in the first line. To a human, the italics probably indicate that the word is stressed; Prosodic, though, does not see typeface. To my ear, the poem also follows a loose ballad meter, with the 4/3 beat structure rendered as 7 stresses per line---but it is so irregular that it does not match very well with any of the four metrical feet Prosodic tracks. These are just two examples of metrical complexity that our project does not capture.

⁹ Properly speaking, the most accurate measure would be a Hood Vector. Vectors include information about direction, so they would show whether a poem was far from Hood by virtue of occupying the iambic corner, the dactylic corner, the boundary between anapest and dactyl, etc. With this accuracy, however, comes a tradeoff in ease of understanding and use; e.g., although we can envision Hood Distance as a very promising pedagogical tool in explaining how meter works, it loses some of its appeal if English students are expected to calculate vectors.